Machine Learning   »   Pendahuluan   ›  Beberapa Cara Mendeteksi Outlier (Pencilan) dalam Data Statistik

Beberapa Cara Mendeteksi Outlier (Pencilan) dalam Data Statistik

Ada banyak metode untuk mendeteksi outlier. Dalam tulisan ini, kita akan membahas cara pendeteksian outlier menggunakan pendekatan metode statistik seperti Histogram, Z-Score, Box Plot, dan Inter Quantile Range (IQR).

---

Outline Artikel:

• Bagaimana mendeteksi outlier?
• Mendeteksi outlier dengan pendekatan statistik
• Mendeteksi outlier melalui histogram
• Mendeteksi outlier dengan metode Z-Score/Maksimum Likelihood
• Mendeteksi outlier melalui Box Plot
• Mendeteksi outlier berdasarkan Inter Quartile Range (IQR)

Oleh Iman Jihad Fadillah · Statistisi

3 Januari 2023

Seperti yang sudah dibahas pada tulisan sebelumnya, outlier atau pencilan adalah objek data yang menyimpang secara signifikan dari objek lainnya dalam suatu kelompok data. Adanya outlier pada data dapat menyebabkan analisis yang menggunakan metode statistik standar menjadi bias.

Oleh karenanya keberadaan outlier perlu dihindari/ditangani sebelum melakukan proses analisis data. Sebelum menangani outlier, tentunya kita perlu mendeteksi objek mana yang merupakan outlier dan objek mana yang bukan. Pada kesempatan ini, kita akan membahas beberapa cara untuk mendeteksi outlier pada suatu kelompok data.

Bagaimana Mendeteksi Outlier?

Ada banyak metode yang bisa digunakan untuk mendeteksi outlier. Banyak literatur yang membahas metode-metode untuk mendeteksi outlier, dan sebagian dalam pembahasan metode deteksi outlier, membuat asumsi tentang outlier versus data lainnya. Berdasarkan asumsi tersebut, kita dapat mengategorikan metode pendeteksian outlier menjadi tiga jenis, yaitu metode statistik, metode proximity-based, dan metode berbasis clustering.

Beberapa metode lain yang juga dibahas yaitu metode pendeteksian outlier menggunakan pendekatan berbasis Supervised, Semi-Supervised, dan Unsupervised Methods. Penggunaan metode-metode tersebut memanfaatkan pembangunan model atau training dataset dalam mendeteksi outlier.

Mendeteksi Outlier dengan Pendekatan Statistik

Dalam tulisan ini, kita akan membahas cara mendeteksi outlier menggunakan pendekatan metode statistik. Metode statistik (juga dikenal sebagai metode berbasis model) membuat asumsi normalitas data. Mereka berasumsi bahwa objek data normal dihasilkan oleh model statistik (stokastik), dan data yang tidak mengikuti model adalah outlier.

Beberapa cara mendeteksi outlier dengan pendekatan metode statistik antara lain, Histogram, Z-Score/Maximum likelihood, Box Plot, dan Inter Quantile Range (IQR).

Mari kita bahas masing-masing cara mendeteksi outlier tersebut berikut ini.

Histogram

Kita dapat menggunakan histogram sebagai model statistik nonparametrik untuk menangkap outlier. Melalui visualisasi histogram, kita bisa melihat secara subjektif, data-data yang termasuk outlier atau tidak.

Contoh 1:

Kelompok data yang terdiri dari 28 siswa/siswi, memiliki rata-rata tinggi badan (cm) sebesar 156,43 cm. Adapun tinggi masing-masing orang adalah sebagai berikut:

Dari kelompok ini, akan dibuat histogram untuk mengidentifikasi outlier di kelompok ini. Adapun histogram dari 28 siswa tersebut adalah sebagai berikut:

Dari hasil histogram tersebut, semua data terlihat berdistribusi cukup normal dan tidak terlihat anomali.

Kemudian pada kelompok tersebut bergabung 2 orang siswa yang memiliki tinggi badan outlier, dengan tinggi badan masing-masing sebesar 100 cm, dan 210 cm. Berikut bentuk histogram baru untuk kelompok tersebut.

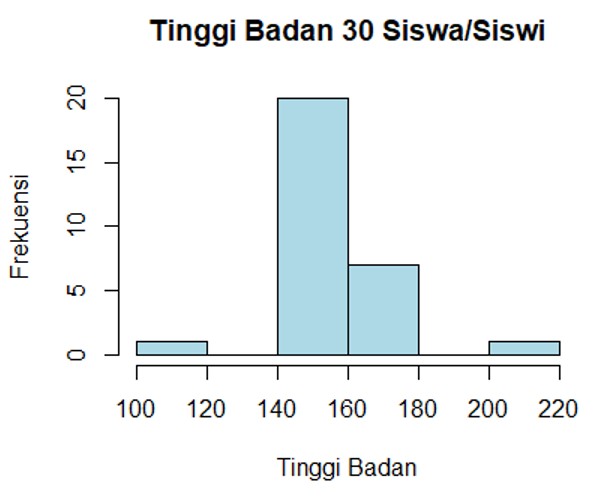
Dari histogram ini, terlihat ada 2 bar (batang) histogram yang berbeda posisi cukup jauh dengan bar histogram lain, yang menunjukkan bahwa kedua data tersebut merupakan data outlier.

Z-Score

Metode Z-score untuk mendeteksi outlier memanfaatkan nilai rata-rata dan standar deviasi atau simpangan baku. Adapun rata-rata dan simpangan baku dirumuskan sebagai berikut:

\begin{aligned} \hat{\mu} = \bar{x} &= \frac{1}{n} \sum_{i=1}^n x_i \\[8pt] \hat{\sigma} &= \sqrt{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2 } \end{aligned}

di mana: \( \hat{\mu} = \bar{x} \) = rata-rata; \( \hat{\sigma} \) = standar deviasi; \( x_i \) = nilai ke-i; \( n \) = jumlah observasi/data.

Sederhananya saja, suatu objek/data dikatakan outlier jika jaraknya lebih dari 3 kali standar deviasi dari nilai rata-ratanya. Untuk lebih mudah dan lebih cepat mendeteksi outlier, maka digunakan Z-score yang diperoleh melalui rumus sebagai berikut:

\[ Z-score = \frac{x-\bar{x}}{\hat{\sigma}} \]

di mana: \(x\) = nilai objek/data yang diperiksa

Suatu data dikatakan outlier jika nilai Z-score kurang dari \(-3\) atau lebih besar dari \(+3\).

Contoh 2:

Dengan menggunakan data yang sama pada Contoh 1, kita akan melakukan perhitungan nilai Z-score untuk tinggi badan 30 siswa tersebut.

Dari data tinggi badan di atas, diperoleh rata-rata sebesar 156,35 cm dan standar deviasi sebesar 15,44, sehingga dari hasil ini diperoleh Z-score untuk masing-masing objek/data adalah sebagai berikut:

Berdasarkan hasil perhitungan Z-Score, terlihat ada dua objek/data atau 2 orang siswa yang memiliki nilai kurang dari \(-3\) atau lebih dari \(+3\) sehingga merupakan nilai outlier. Hasil ini sama dengan hasil pada Contoh 1.

Box Plot

Kita juga dapat mengidentifikasi outlier dengan memanfaatkan visualisasi dari Box-Plot. Melalui visualisasi Boxplot, kita bisa melihat secara objektif, data-data mana yang termasuk outlier atau tidak. Boxplot memanfaatkan nilai kuartil pada data (Q1, Q2 atau median, dan Q3), serta nilai minimum dan maksimum (tata-cara membuat garis boxplot akan dibahas pada pembahasan Inter Quantile Range (IQR).

Contoh 3:

Menggunakan data yang sama dengan Contoh 1, maka diperoleh gambaran boxplot sebagai berikut:

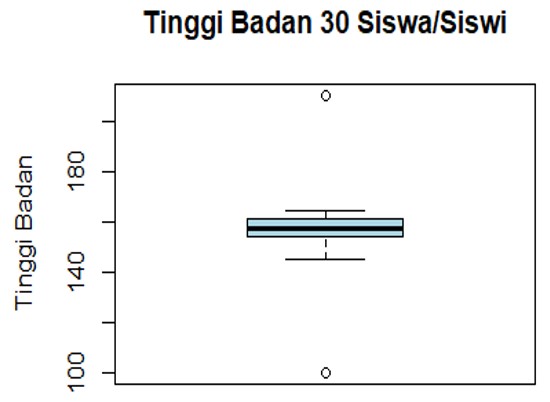
Dari hasil ini terlihat ada dua nilai yang merupakan outlier, ditandai dengan titik/bulatan yang melebihi batas atas dan bawah boxplot. Dari hasil ini terlihat outlier adalah siswa dengan tinggi 100 cm dan 210 cm, serupa dengan hasil pembahasan pada Contoh 1 dan Contoh 2.

Kelemahan dari cara deteksi outlier melalui boxplot adalah jika outlier yang muncul cukup banyak, maka titik-titik akan menumpuk dan jumlah outlier kurang bisa tergambarkan secara rill.

Inter Quantile Range (IQR)

Penentuan suatu objek merupakan outlier atau tidak pada cara ini saling berhubungan dengan penentuan outlier menggunakan boxplot. Penentuan outlier mengunakan IQR memanfaatkan nilai kuartil pada data (Q1, Q2 atau median, dan Q3), serta nilai minimum dan maksimum pada data. Nilai IQR didefinisikan sebagai:

\[ IQR = Q_3 - Q_1 \]

Suatu data dikatakan outlier jika data tersebut lebih kecil dari \[ \text{batas bawah} = Q_1-1,5 \cdot IQR \] atau lebih dari \[ \text{batas atas} = Q_3+1,5 \cdot IQR \]

Cara ini berhubungan dengan boxplot, karena batas bawah boxplot adalah nilai minimum (jika tidak kurang dari \(Q_1-1,5 \cdot IQR\)), dan batas atas adalah nilai maksimum (jika tidak lebih dari \(Q_3+1,5 \cdot IQR\)). Sedangkan jika berada di luar rentang tersebut, maka batas atas dan batas bawah akan mengikuti kedua nilai yang dirumuskan di atas. Sementara kotak-kotak pada boxplot terbentuk dari batasan nilai Q1, Q2 atau median, dan Q3.

Contoh 4:

Menggunakan data yang sama dengan Contoh 1, dilakukan perhitungan batas atas dan batas bawah untuk masing masing tinggi badan (cm) siswa/siswi. Adapun nilai tinggi badan 30 siswa dapat dilihat pada Contoh 2. Dari data tersebut, diperolah nilai batas bawah dan batas atas sebagai berikut:

Dari hasil ini diperoleh data normal dan outlier sesuai urutan adalah sebagai berikut:

Perhatikan bahwa dari tinggi badan 30 siswa yang termasuk outlier adalah siswa dengan tinggi badan 100 cm (karena kurang dari batas bawah 143,875) dan 210 cm (karena lebih dari batas atas 170,875). Hasil yang kita peroleh ini serupa dengan pembahasan pada Contoh 1, Contoh 2 dan Contoh 3.

Perlu diingat, walaupun hasil pendeteksian outlier dari keempat metode di atas menunjukkan hasil yang serupa, hasil outlier menggunakan cara yang berbeda tidak selalu menunjukkan hasil yang sama.

Sumber:

Han, J., & Kamber, M. (2012). Data Mining: Concepts and Techniques. Elsevier.

Editor: Tju Ji Long · Statistisi