www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Bahas Soal Matematika   »   Vektor & Ruang Vektor   ›  Contoh Soal Perkalian Titik Vektor
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Contoh Soal Perkalian Titik Vektor

Pada tulisan ini kita akan mempelajari cara menghitung perkalian titik vektor (dot product) disertai contoh soal dan pembahasannya. Jika diketahui \( \vec{u} = (u_1,u_2,u_3) \) dan \( \vec{v} = (v_1,v_2,v_3) \) adalah vektor-vektor pada ruang 3 dimensi dan \( \theta \) adalah sudut di antara kedua vektor tersebut, maka rumus perkalian titik vektor \( \vec{u} \) dan \( \vec{v} \), yaitu:

rumus perkalian vektor
Contoh 1:

Jika \( \vec{a} = 4 \hat{i}+\hat{j}+5 \hat{k} \) dan \( \vec{b} = 2 \hat{i}+\hat{j}-5 \hat{k} \) maka hasil kali \( \vec{a} \cdot \vec{b} = \cdots \)

  1. \( -18 \)
  2. \( -16 \)
  3. \( 3 \)
  4. \( 12 \sqrt{5} \)
  5. \( 18 \sqrt{6} \)
Pembahasan »

Dari informasi yang diberikan dalam soal, kita peroleh berikut:

\begin{aligned} \vec{a} \cdot \vec{b} &= (4, 1, 5) \cdot (2, 1, -5) \\[8pt] &= (4)(2)+(1)(1)+(5)(-5) \\[8pt] &= 8+1-25 \\[8pt] &= -16 \end{aligned}

Jawaban B.

Contoh 2:

Jika \( A(2,-3,4), \ B(6,-2,2) \) dan \( C(5,4,3) \) adalah titik-titik sudut dari segitiga ABC maka nilai \( \overrightarrow{AB} \cdot \overrightarrow{BC} = \cdots \)

  1. \( -8 \)
  2. \( 0 \)
  3. \( 6 \)
  4. \( 12 \)
  5. \( 15 \sqrt{3} \)
Pembahasan »

Berdasarkan apa yang diberikan pada soal, kita peroleh berikut:

\begin{aligned} \overrightarrow{AB} &= B - A = (6, -2, 2) - (2, -3, 4) \\[8pt] &= (4, 1, -2) \\[8pt] \overrightarrow{BC} &= C - B = (5, 4, 3) - (6,-2,2) \\[8pt] &= (-1,6,1) \\[8pt] \overrightarrow{AB} \cdot \overrightarrow{BC} &= (4, 1, -2) \cdot (-1,6,1) \\[8pt] &= (4)(-1)+(1)(6)+(-2)(1) \\[8pt] &= -4+6-2 \\[8pt] &= 0 \end{aligned}

Jawaban B.

Contoh 3:

Diketahui \( A(4,-3,2) \) dan \( B(-2,5,0) \). Jika titik \( P \) berada di tengah-tengah \(AB\), maka nilai dari \( \overrightarrow{PA} \cdot \overrightarrow{PB} = \cdots \)

  1. \( 8 \)
  2. \( 3 \)
  3. \( -6 \)
  4. \( -20 \)
  5. \( -26 \)
Pembahasan »

Karena titik P berada di tengah-tengah AB maka koordinat \( P \left( \frac{4-2}{2}, \frac{-3+5}{2}, \frac{2+0}{2} \right) \) atau \( P(1,1,1) \). Selanjutnya, kita peroleh berikut ini:

\begin{aligned} \overrightarrow{PA} &= A-P = (4, -3, 2)-(1,1,1) \\[8pt] &= (3, -4, 1) \\[8pt] \overrightarrow{PB} &= B-P = (-2, 5, 0)-(1,1,1) \\[8pt] &= (-3, 4, -1) \\[8pt] \overrightarrow{PA} \cdot \overrightarrow{PB} &= (3, -4, 1) \cdot (-3, 4, -1) \\[8pt] &= (3)(-3)+(-4)(4)+(1)(-1) \\[8pt] &= -9-16-1 \\[8pt] &= -26 \end{aligned}

Jawaban E.

Contoh 4:

Diketahui \( A(1,0,-1), B(2,-5,2) \) dan \( C(-3,1,0) \) maka nilai dari \( \overrightarrow{BC} \cdot \left( \overrightarrow {AC}+2\overrightarrow {AB} \right) = \cdots \)

  1. \( 78 \)
  2. \( 64 \)
  3. \( 58 \)
  4. \( -58 \)
  5. \( -78 \)
Pembahasan »

Berdasarkan apa yang diberikan pada soal, kita peroleh berikut:

\begin{aligned} \overrightarrow{BC} &= C-B = (-3,1,0)-(2,-5,2) \\[8pt] &= (-5,6,-2) \\[8pt] \overrightarrow{AC} &= C-A = (-3,1,0)-(1,0,-1) \\[8pt] &= (-4,1,1) \\[8pt] \overrightarrow{AB} &= B-A = (2,-5,2)-(1,0,-1) \\[8pt] &= (1,-5,3) \\[8pt] 2 \overrightarrow{AB} &= 2 (1,-5,3) = (2,-10,6) \end{aligned}

Selanjutnya, dari hasil di atas, maka kita dapatkan berikut ini:

\begin{aligned} \overrightarrow{BC} \cdot \left( \overrightarrow{AC}+2\overrightarrow{AB} \right) &= (-5,6,-2) \cdot ((-4,1,1)+(2,-10,6)) \\[8pt] &= (-5,6,-2) \cdot (-2,-9,7) \\[8pt] &= (-5)(-2)+(6)(-9)+(-2)(7) \\[8pt] &= 10-54-14 \\[8pt] &= -58 \end{aligned}

Jawaban D.

Contoh 5:

Diketahui vektor \( \vec{a} = 3 \hat{i}-4\hat{j}+2\hat{k} \) dan \( \vec{b} = 2 \hat{i}+3\hat{j} \) serta \( \vec{c} = 4 \hat{i}+\hat{j}-6\hat{k} \), maka hasil dari \( 2 \vec{a} \left( 3 \vec{b}-2 \vec{c} \right) = \cdots \)

  1. \( -24 \)
  2. \( -20 \)
  3. \( 8 \)
  4. \( 12 \)
  5. \( 18 \)
Pembahasan »

Berdasarkan informasi yang diberikan pada soal, kita peroleh berikut:

\begin{aligned} \vec{a} \cdot \vec{b} &= (3, -4, 2) \cdot (2, 3, 0) \\[8pt] &= (3)(2)+(-4)(3)+(2)(0) \\[8pt] &= -6 \\[8pt] \vec{a} \cdot \vec{c} &= (3, -4, 2) \cdot (4, 1, -6) \\[8pt] &= (3)(4)+(-4)(1)+(2)(-6) \\[8pt] &= -4 \\[8pt] 2 \vec{a} \left( 3 \vec{b}-2 \vec{c} \right) &= (2)(3) \vec{a} \cdot \vec{b} - (2)(2) \vec{a} \cdot \vec{c} \\[8pt] &= (6)(-6)-(4)(-4) \\[8pt] &= -36+16 \\[8pt] &= -20 \end{aligned}

Jawaban B.

Contoh 6:

Diketahui segitiga ABC di mana \( A(2x, 7, 3), B(x, 7, 7) \) dan \( C(10,16,3x) \). Jika segitiga ABC siku-siku di A maka nilai \(x= \cdots\)

  1. \( -5 \)
  2. \( -4 \)
  3. \( 1 \)
  4. \( 2 \)
  5. \( 4 \)
Pembahasan »

Pertama, kita cari dulu vektor \( \overrightarrow{AB} \) dan \( \overrightarrow{AC} \), yakni:

\begin{aligned} \overrightarrow{AB} &= B - A = (x, 7, 7) - (2x,7,3) \\[8pt] &= (x-2x, \ 7-7, \ 7-3) = (-x, \ 0, \ 4) \\[8pt] \overrightarrow{AC} &= C - A = (10,16,3x) - (2x,7,3) \\[8pt] &= (10-2x, \ 16-7, \ 3x-3) = (10-2x, \ 9, \ 3x-3) \end{aligned}

Karena segitiga ABC siku-siku di A maka sudut \( \overrightarrow{AB} \) dan \( \overrightarrow{AC} \) adalah \( 90^\circ \) sehingga berlaku:

\begin{aligned} \overrightarrow{AB} \cdot \overrightarrow{AC} &= 0 \\[8pt] (-x, \ 0, \ 4) \cdot (10-2x, \ 9, \ 3x-3) &= 0 \\[8pt] (-x)(10-2x)+(0)(9)+(4)(3x-3) &= 0 \\[8pt] -10x+2x^2+0+12x-12 &= 0 \\[8pt] 2x^2+2x-12 &= 0 \\[8pt] x^2+x-6 &= 0 \\[8pt] (x+3)(x-2) &= 0 \\[8pt] x = -3 \ \text{atau} \ x &= 2 \end{aligned}

Jawaban D.

Contoh 7:

Jika vektor \( \vec{a}+\vec{b}+\vec{c} = 0 \) dan \( | \vec{a} | = 3, \ | \vec{b} | = 5 \) dan \( | \vec{c} | = 7 \), maka nilai \( \vec{a} \cdot \vec{b} = \cdots \)

  1. \( 225 \)
  2. \( 200 \)
  3. \( 125 \)
  4. \( 75,5 \)
  5. \( 7,5 \)
Pembahasan »

Berdasarkan informasi yang diberikan pada soal, maka kita peroleh berikut:

\begin{aligned} \vec{a}+\vec{b}+\vec{c} = 0 \Leftrightarrow \vec{a}+\vec{b} &= -\vec{c} \\[8pt] \left( \vec{a}+\vec{b} \right)^2 &= (-\vec{c})^2 \\[8pt] \vec{a} \cdot \vec{a} + 2 \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{b} &= \vec{c} \cdot \vec{c} \\[8pt] |\vec{a}|^2+ 2 \vec{a} \cdot \vec{b} + |\vec{b}|^2 &= |\vec{c}|^2 \\[8pt] 3^2+2\vec{a}\cdot \vec{b}+5^2 &= 7^2 \\[8pt] 9+2\vec{a}\cdot \vec{b} + 25 &= 49 \\[8pt] 2 \vec{a} \cdot \vec{b} &= 49-34 \\[8pt] \vec{a}\cdot \vec{b} &= \frac{15}{2} = 7,5 \end{aligned}

Jawaban E.

Contoh 8:

Diketahui koordinat \( P(-3,2,1) \) dan \( Q(7,-3,11) \). Jika titik R membagi PQ dengan perbandingan \( \overrightarrow{PR}: \overrightarrow{RQ} = 3:2 \) maka \( \overrightarrow{PR} \cdot \overrightarrow{RQ} = \cdots \)

  1. \( 54 \)
  2. \( 36 \)
  3. \( 30 \)
  4. \( 24 \)
  5. \( 20 \)
Pembahasan »

Karena \( \overrightarrow{PR}: \overrightarrow{RQ} = 3:2 \) maka kita peroleh berikut:

\begin{aligned} 2 \overrightarrow{PR} &= 3 \overrightarrow{RQ} \\[8pt] 2 (\vec{r}-\vec{p}) &= 3 (\vec{q}-\vec{r}) \\[8pt] 2\vec{r}-2\vec{p} &= 3\vec{q}-3\vec{r} \\[8pt] 5\vec{r} &= 2\vec{p}+3\vec{q} \\[8pt] 5 \vec{r} &= 2(7, -3, 11)+3(-3,2,1) \\[8pt] 5 \vec{r} &= (14, -6, 22)+(-9, 6, 3) \\[8pt] 5 \vec{r} &= (5, 0, 25) \Rightarrow \vec{r} = (1,0,5) \\[8pt] \overrightarrow{PR} &= \vec{r}-\vec{p} = (1,0,5) - (-3,2,1) \\[8pt] &= (4, -2, 4) \\[8pt] \overrightarrow{RQ} &= \vec{q}-\vec{r} = (7, -3, 11)-(1,0,5) \\[8pt] &= (6,-3,6) \end{aligned}

Selanjutnya, dari hasil di atas, kita peroleh:

\begin{aligned} \overrightarrow{PR} \cdot \overrightarrow{RQ} &= (4, -2, 4) \cdot (6, -3, 6) \\[8pt] &= (4)(6)+(-2)(-3)+(4)(6) \\[8pt] &= 24+6+24 \\[8pt] &= 54 \end{aligned}

Jawaban A.

Contoh 9:

Suatu persegi panjang OABC diketahui nilai \( |\overrightarrow{OA}| = 12 \) cm dan \( |\overrightarrow{AB}| = 5 \) cm. Jika \( |\overrightarrow{OA}| = \vec{a} \) dan \( |\overrightarrow{OB}| = \vec{b} \), maka nilai \( \vec{a} \cdot ( \vec{a}+\vec{b} ) = \cdots \)

  1. \( 288 \)
  2. \( 144 \)
  3. \( 72 \)
  4. \( -36 \)
  5. \( -72 \)
Pembahasan »

Untuk memudahkan, kita bisa gambar persegi panjang OABC sebagai berikut:

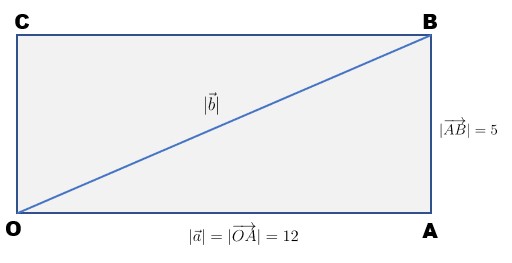
contoh perkalian titik vektor

Dari gambar persegi panjang di atas, dengan menggunakan teorema pitagoras kita peroleh berikut:

\begin{aligned} |\overrightarrow{OB}|^2 &= |\overrightarrow{OA}|^2+|\overrightarrow{AB}|^2 \\[8pt] |\vec{b}|^2 &= 12^2+5^2 \\[8pt] |\vec{b}| &= \sqrt{144+25} = \sqrt{169} \\[8pt] &= 13 \end{aligned}

Dengan demikian, kita peroleh:

\begin{aligned} \vec{a} \cdot (\vec{a}+\vec{b}) &= \vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} \\[8pt] &= |\vec{a}|^2+|\vec{a}||\vec{b}| \cos AOB \\[8pt] &= 12^2+(12)(13) \cdot \frac{12}{13} \\[8pt] &= 144+144 \\[8pt] &= 288 \end{aligned}

Jawaban A.

Cukup sekian untuk artikel ini. Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Penulis: Tju Ji Long · Statistisi

Artikel Terkait
img

Contoh soal menghitung panjang vektor

img

Contoh soal menghitung sudut antara dua vektor