
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Integral › Integral trigonometri Berpangkat
Tentukan hasil dari \(\int \cos^2 x \ dx = \cdots ? \)
Pembahasan:
Untuk menyelesaikan integral ini kita perlu ganti fungsi \( \cos^2 x \) ke bentuk lain yang bisa diintegralkan. Dengan menggunakan rumus identitas trigonometri, kita peroleh hasil berikut:
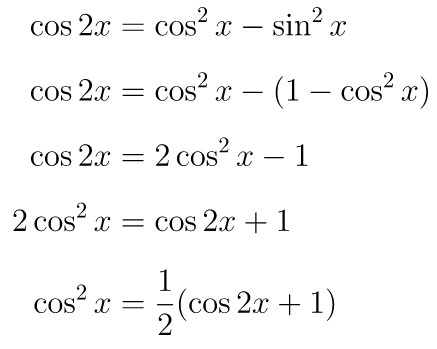
Selanjutnya, dengan menggunakan hasil yang kita peroleh di atas, maka penyelesaian integral dalam soal yaitu:
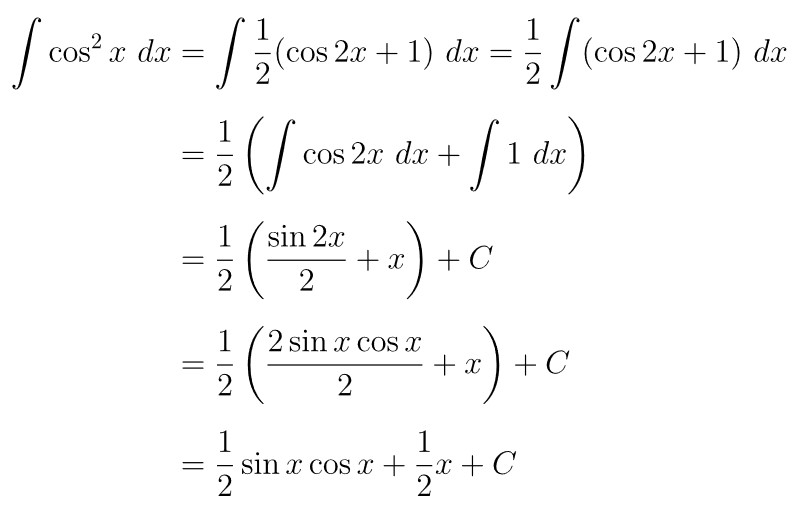
Rumus Integral Trigonometri Berpangkat
Berikut ini adalah beberapa rumus terkait integral trigonometri berpangkat:


Untuk integral trigonometri pangkat yang lebih tinggi kita dapat gunakan rumus reduksi berikut ini. Untuk pembuktiannya klik ini: Rumus Reduksi Integral Trigonometri
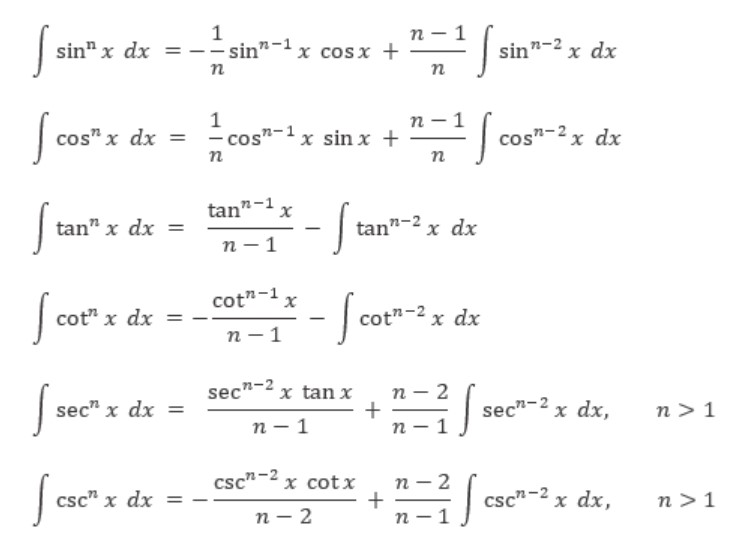
Baca juga:
\( \displaystyle \int \cos x \ dx = \cdots ? \)
\( \displaystyle \int \cos^3 x \ dx = \cdots ? \)
\( \displaystyle \int \cos^4 x \ dx = \cdots ? \)
\( \displaystyle \int \cos^5 x \ dx = \cdots ? \)