www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Geometri › Contoh Soal Menentukan Persamaan Bola dan Pembahasannya
Contoh Soal Menentukan Persamaan Bola dan Pembahasannya
Pada artikel ini kita akan mempelajari cara menentukan persamaan bola yang berpusat di titik pusat O(0,0,0) dan berjari-jari r dan persamaan bola yang berpusat di titik M(a,b,c) dengan jari-jari r. Selain itu, kita juga akan menentukan titik pusat dan jari-jari bola jika diketahui persamaan bola tersebut.
Rumus persamaan bola yang berpusat di O(0,0,0) dan berjari-jari \(r\) adalah
Rumus persamaan bola yang berpusat di M(a,b,c) dan berjari-jari \(r\) adalah
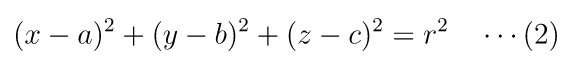
Rumus (2) di atas dapat diperluas menjadi:
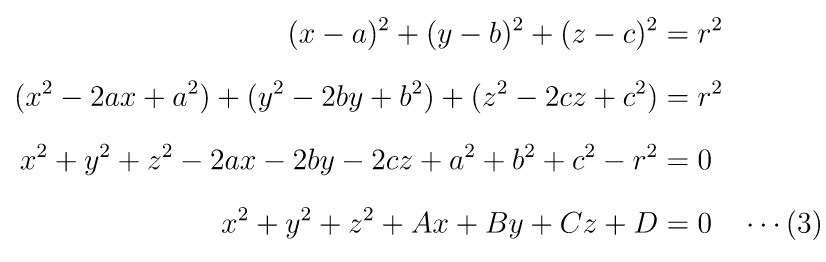
di mana:
Persamaan (3) di atas disebut bentuk umum dari persamaan bola.
Rumus untuk menentukan titik pusat dan jari-jari bola, yaitu:
Contoh 1:
Tentukan persamaan bola yang berpusat di titik O(0,0,0) dengan jari-jari 5 satuan.
Pembahasan »Berdasarkan rumus (1) di atas, persamaan bola dengan titik pusat O(0,0,0) dan berjari-jari 5 satuan, yaitu:
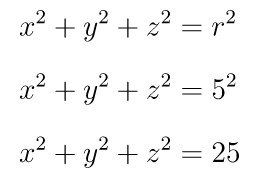
Contoh 2:
Tentukan persamaan bola yang berpusat di titik (-6,2,-3) dan berjari-jari 2 satuan.
Pembahasan »Dengan melihat rumus (2) dan (3) di atas, maka persamaan bola yang berpusat di titik (-6,2,-3) dengan jari-jari 2 satuan, yaitu:
Contoh 3:
Tentukan persamaan bola yang berpusat di titik M(1,2,3) dan melalui titik (2,4,1).
Pembahasan »Pertama, tentukan dulu jari-jari bolanya. Jari-jari bola adalah jarak dua titik yang diketahui tersebut, yakni:
Selanjutnya, substitusikan jari-jari bola yang diperoleh di atas dan titik pusat M(1,2,3) ke bentuk umum persamaan bola, sehingga:
Jadi, persamaan bola yang berpusat di M(1,2,3) dan melalui titik (2,4,1) adalah:
Contoh 4:
Tentukan titik pusat dan jari-jari bola yang persamaannya adalah:
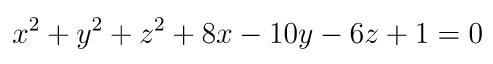Pembahasan »
Dari persamaan bola di atas, diperoleh A = 8, B = -10, C = -6, dan D = 1 sehingga:
Dengan demikian, titik pusat bolanya adalah M(a,b,c) = M(-4,5,3).
Selanjutnya, karena \( a^2+b^2+c^2-r^2 = D \), maka
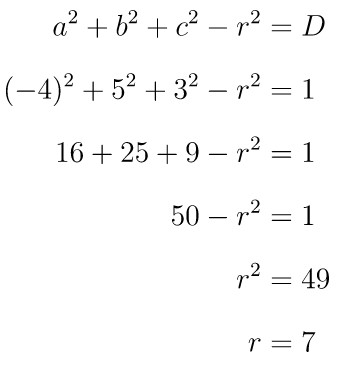
Jadi, titik pusat dan jari-jari dari bola dengan persamaan \( x^2+y^2+z^2+8x-10y-6z+1=0 \) adalah M(-4,5,3) dan r = 7.
Cukup sekian untuk artikel ini. Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Penulis: Tju Ji Long · Statistisi